Addressing Objects in Java Applications

About Object Names in the Object Browser

Addressing Java Objects Using Name Mapping and Aliases

Addressing Java Objects Without Name Mapping

Note for AWT and Swing Applications Users

Combining Mapped and Unmapped Object Names

Accessing Non-Visual Objects in Java Applications

Further Reading

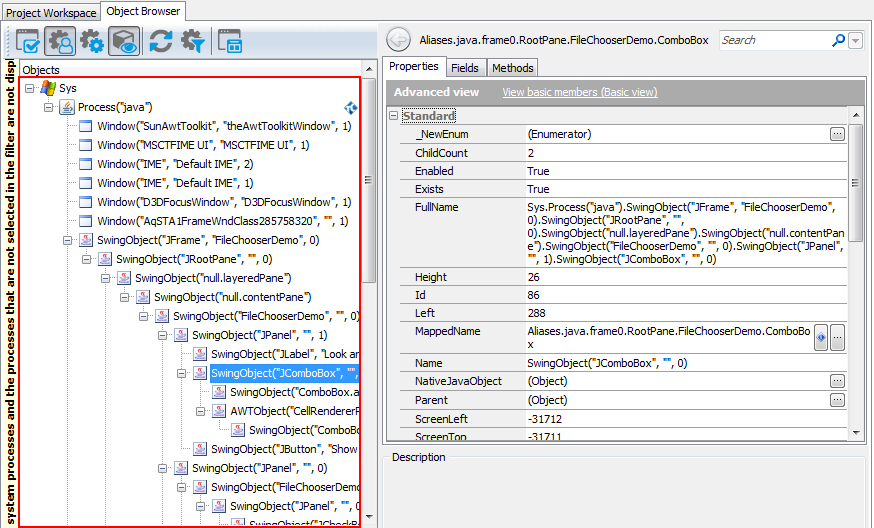
You can explore the object structure of the tested application in the Object Browser. Here is a sample view of the Java application hierarchy displayed in the Object Browser:

Click the image to enlarge it.

Here, the Process("java") branch of the Sys object corresponds to your tested Java application and the other objects correspond to the application’s windows, controls and objects.

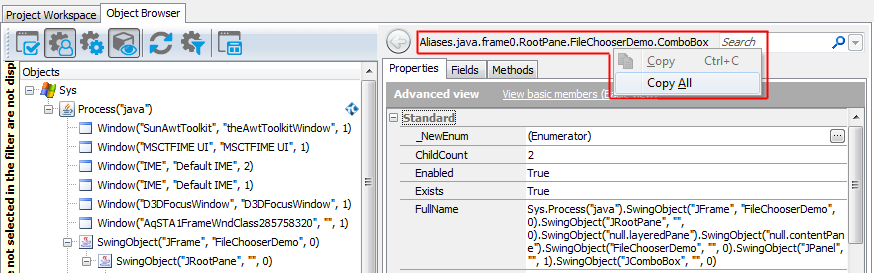
To refer to an individual object in the tested Java application, select the needed object in the Object Browser or Object Spy. These tools display the selected object’s name above the member list. From the right-click menu, you can copy this name to the clipboard and then insert it into your test.

Click the image to enlarge it.

You may notice that this name differs from what you see in the object tree on the left of the Object Browser. This is because the name displayed at the top of the panel uses object aliases, if they are defined, whereas the object tree uses the naming syntax that includes identification properties. The differences between the two object naming syntaxes are explained in the Addressing Java Objects Using Name Mapping and Aliases and Addressing Java Objects Without Name Mapping sections below.

You can also learn the object names in different syntaxes by looking at the following object properties:

• MappedName - the object’s fully-qualified alias (including the aliases of all parent objects). This name is used for the object by default in your tests. Note that if the selected object is not in Name Mapping, this property is empty.

• Name - the object name that includes the object's identification properties. This is the same name you see in the Object Browser’s object tree. For an explanation of this syntax, see below.

• FullName - the object’s fully-qualified name that includes the object's identification properties. This name consists of the object’s Name property value and the Names property value of all of the object's parent objects. See below.

By default, TestComplete uses object names from Name Mapping (the object repository) to refer to individual objects in Java applications under test. These names are called aliases. When you are recording a test, TestComplete automatically adds the recorded objects to Name Mapping and generates aliases for them.

You can see the available object aliases and add new aliases in the Name Mapping editor.

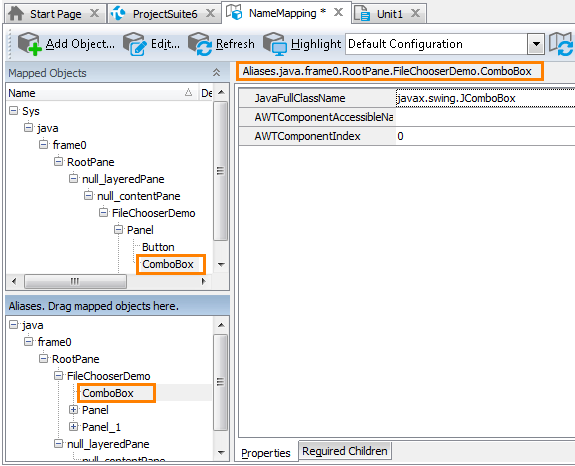
Here, Mapped Objects and Aliases display the hierarchy of mapped objects and their aliases, respectively. The fully-qualified alias that can be used to refer to an object is displayed in the top right part of the Name Mapping editor (see the image above). It starts with Aliases and includes aliases of all of the object’s parent objects separated by dots (in VBScript, JScript, Python and DelphiScript projects) or square brackets (in C++Script and C#Script projects). For example, in the image above you can see that you can refer to the ComboBox object using the following name:

You can copy object aliases from the Name Mapping editor to the clipboard and use them when manually adding test operations over the tested application’s objects.

The following example shows a sample item selection operation on the ComboBox combo box control specified by an alias:

Note that the fully-qualified mapped name for this object is the following:

Since the null_layeredPane, null_contentPane and Panel objects are of no interest for our test, we exclude them from the path to the ComboBox object in the Alias tree, so the object hierarchy becomes shorter. Using aliases lets you make your scripts shorter and more readable.

For more information about using Name Mapping and aliases, see Name Mapping and Access Objects by Aliases.

Your tests can work not only with applications and objects added to Name Mapping, but also with any other running applications, their windows and controls. These objects can be addressed using a syntax that directly includes identification property values.

Consider the following sample code and keyword test that illustrate how you can refer to an object in your Java application:

To learn the exact syntax for referring to a particular object, use the Object Browser - the object tree and the FullName property of objects always use this naming syntax. See the About Object Names in the Object Browser section above.

Let’s have a closer look at this notation and its components.

• The notation starts with the Sys object that represents the operating system.

• The next object, Process("java"), corresponds to a Java virtual machine on which the Java code is executed.

• The other objects represent windows and visual objects in the application. Depending on the Java library, the default syntax for these objects is as follows:

  SwingObject(NativeName)
  

  AWTObject(NativeName)
  

  SWTObject(NativeName)
  

  • The SwingObject notation is used in Java applications that use the Swing library; the SWTObject notation - for Java applications that use the SWT library; AWTObject - for Java applications that use the AWT library.
  • NativeName is the object name as it is specified in the tested application’s source code (the string that is returned by the object’s getName method).

  Another possible syntax for Java objects is:

  SwingObject(JavaClassName, AccName, [Index])
  

  SWTObject(JavaClassName, AccName, [Index])
  

  AWTObject(JavaClassName, AccName, [Index])
  

  Instead of the object’s native name, it uses its Java class name (the short class name as it is specified in the application’s code), accessible window caption (the value returned by the javax.accessibility.AccessibleContext.getAccessibleName method) and (optionally) index among sibling objects with the same class and text.

  The Index parameter is used only if the object contains two or more child objects that have the same class name and caption.

  This syntax is used in the following cases:

  • TestComplete cannot determine the object name that is specified in the application code.

  • There are several objects with the same name.

  Note:

  To address windows of AWT and Swing applications, you may also need the fourth parameter called WndIndex. It is used in rare cases when the other three parameters of one window coincide with the appropriate parameters of another window (see below).

  For more information about Java object addressing syntax and its parameters, see the description of the AWTObject, SWTObject and SwingObject notations.

For examples of this syntax applied to objects in your tested Java application, examine your application in the Object Browser. You can also copy this syntax from the Object Browser and paste it to your test in order not to manually type it.

Remarks

To address controls of an AWT or Swing application, TestComplete may also use the window index in addition to the class name, an accessible name and the control’s index. In some situations, TestComplete may "think" that a window contains several controls that have the same class name, accessible name and index. In this case, TestComplete uses one extra parameter - window index - to uniquely identify such controls. The parameter value coincides with the value of the Index property. This happens only if the following conditions are met:

• The addressed component is a windowed component.

-- and --

• One of the following conditions are met:
  • The addressed component has a parent Java component (not parent window, but the parent component in Java terms, that is, the object that is returned by the component’s getParent() method).
      -- and --
    This parent component is not a windowed control (for instance, Box).

  -- or --

  • The addressed component is a top-level window.
      -- and --
    It that has a parent Java component.
      -- and --
    This parent component is a windowed component.

  -- or --

  • The addressed component does not have a parent component in Java terms.

The following figure illustrates these conditions:

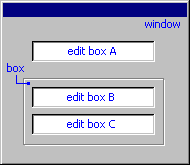
The edit boxes B and C are windowed controls. They lay on a box control, which is a non-windowed control. So, if the edit boxes B and C have the same accessible name, TestComplete additionally uses the window index to address them. TestComplete will not use the window index for the edit box A, since this edit box does not lay on a non-windowed control.

In some rare cases a similar situation may happen to top-level windows, so, to obtain the desired window, you may also need to use the WndIndex parameter. To determine if the parameter is needed, see the window name in the object tree of the Object Browser panel.

The Java group of the project properties has an option that specifies how TestComplete recognizes child objects of spin boxes, combo boxes and other components that contain child controls. See Project Properties - Java Options for more information.

You can combine aliases specified in Name Mapping and the SwingObject (or AWTObject or SWTObject) notation when referencing an object hierarchy in tests. For example, you can use aliases for parent objects and the SwingObject notation for child objects:

However, keep in mind that aliases must always precede the SwingObject notation in the object hierarchy. Aliases cannot be used after the SwingObject notation within the same statement. That is, the following statement is invalid:

Java applications can include non-visual objects that are not displayed in the Object Browser. However, you can access these objects from your tests.

To get access to a non-visual object, you need to find a property, field or method of another object (visual or non-visual) that would return a reference to the desired object. To find the needed property or method, examine the tested Java application in the Object Browser or ask the application developers where you can find it.

Also, you can obtain a reference to the desired object by using a static field, property or method, which you can access via the JavaRuntime(…).JavaClasses statement. JavaRuntime is a method that TestComplete adds to each process initiated by a Java application. The object returned by this method corresponds to an instance of the java.lang.Runtime class of the desired Java virtual machine that exists within a Windows process. This object contains the JavaClasses property added to this object by TestComplete. This property lets you address fields and methods of static classes loaded to the virtual machine by using a simple notation:

The following topics explain how to refer to objects in Java applications while performing some common operations over them: